d3可视化实战03:神奇的superformula
需求驱动实现
前文讲过了D3的数据驱动机制,中间所举的例子都很简单。例如那个demo里面,绑定的数据是一个简单的数组,实现的图元也仅仅是一堆用SVG画的circle。但是现实世界中我们往往会遇到复杂的需求,例如我就遇到了这样一个需求:数据是一个复杂的对象数组,而与之绑定的图元是一个可变图形。该图形可以根据与他绑定的数据中的具体参数,在圆形、方块、三角之间切换,并且要求过渡自然。
面对这个需求,最直接的做法是把圆形、方块、三角用SVG的<circle>圆形标签,<rect>矩形标签以及<polygon>多边形标签来分别实现。具体用D3实现,就是创建一个<g>集合标签作为数据绑定对象,根据数据参数的变化,remove里面的原有图形,add新的图形,从而实现数据驱动的图形更新。但是这种方法有一个很难解决的问题,就是图形切换时的过渡动画很难平滑。因为每个图形都是独立的标签,除了采用淡入淡出之类的过渡方法外,很难想到有什么更好的过渡效果。并且出于对代码简化的考虑,g标签内包裹其他的图形标签的方式,也增加了复杂度。
那么还有其他方案吗?如果能有一个万能图形标签来来实现各种图形,把数据直接绑定给它,那就再好不过了。事实上SVG的<path>路径标签就可以实现这一点。在我之前的文章"d3可视化实战01:理解SVG元素特性"中已经提到,路径功能非常强大几乎可以描绘任何图形。唯一的问题是,如何指定Path的具体参数。对于一般情况,我们可以自己设定参数。而在这里,我打算用一个数学模型来指定path的具体参数,那就是superfomula超级方程式。最终实现的效果果然非常好,动画过渡非常平滑,图元本身也很简单。下面让我们看看这个superfomula究竟是何方神圣吧。
about超级方程式
我们知道,很多数学函数都可以用解析式的方式表示,亦可根据变量和自变量的值在不同坐标系下绘成各种图形。Johan Gielis博士提出了一个函数,可以描述自然界中发现的众多复杂图形和曲线,它就是超级方程式superfomula。
超级方式的解析式如下:
![r\left(\varphi\right) =<br /><br /><br /> \left[<br /><br /><br /> \left|<br /><br /><br /> \frac{\cos\left(\frac{m\varphi}{4}\right)}{a}<br /><br /><br /> \right| ^{n_{2}}<br /><br /><br /> +<br /><br /><br /> \left|<br /><br /><br /> \frac{\sin\left(\frac{m\varphi}{4}\right)}{b}<br /><br /><br /> \right| ^{n_{3}}<br /><br /><br /> \right] ^{-\frac{1}{n_{1}}}<br /><br /><br />](http://upload.wikimedia.org/math/3/7/1/37188eb6e21255282d47addba5118740.png)
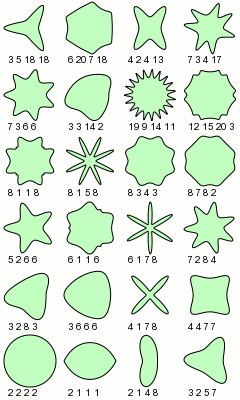
在极坐标系下,r代表半径, 代表角度,a,b,m,n1,n2,n3是可变参数。通过调整参数的值,就可以绘出各种图形。下图展示了a=b=1的情况下,m,n1,n2,n3取不同值的时候superfomula所展示的图形:
代表角度,a,b,m,n1,n2,n3是可变参数。通过调整参数的值,就可以绘出各种图形。下图展示了a=b=1的情况下,m,n1,n2,n3取不同值的时候superfomula所展示的图形:
只通过控制这些参数,就能在极坐标系下绘制如此不同的各种2D图形,是不是很神奇?这就是数学这一自然科学的王冠学科的魅力。
关于superfomula的更多介绍:
superfomula的发表者Johan Gielis博士(1962-)原本的研究方向是园艺工程和生物学。在他的早期研究阶段他就感兴趣于使用数学模型表征生物生长性状。1994年发表的论文中他就开始开始使用曲线描述自然形状,在1997年的论文中他发现广义的曲线模型适用于任何对称形状。在2003年发表于美国植物学杂志上的论文A generic geometric transformation that unifies a large range of natural and abstract shapes中,他提出了superfomula。superfomula是超级椭圆公式superellipse的扩展,但具有更广泛的实用性。此后数百篇论文都引用了superfomula,并且以superfomula为指导的计算机绘图程序也随之出现。2004年johan Gielis博士收到了InterTech技术创新卓越奖,该奖主要颁发给对平面艺术及相关产业产生重大影响的技术发明。superfomula从生物技术研究中诞生,在数学领域中升华,并最终应用到计算机、平面设计等领域。可谓是跨学科研究应用的最好案例之一。
superfomula也可以扩展到3维,4维甚至更多维度。例如3维情况下,图形可以通过两个superfomula r1, r2来生成。其极坐标系与笛卡尔坐标系之间转换关系为:
其中,
变量值域为[ -π/2 , π/2] (latitude维度), θ变量值域为 [ -π, π] (longitude精度).
案例及代码实现
在github上,已经有人用D3实现了基于superfomula的图形绘制程序。大家请点击这里:http://bl.ocks.org/mbostock/1021103. 该程序的关键是基于D3的superfomula开源插件。本着学习的目的,这里保存了该插件的源码,你可以复制它然后保存为d3-superfomula.js来使用:
(function() {
var _symbol = d3.svg.symbol(),
_line = d3.svg.line();
d3.superformula = function() {
var type = _symbol.type(),
size = _symbol.size(),
segments = size,
params = {};
function superformula(d, i) {
var n, p = _superformulaTypes[type.call(this, d, i)];
for (n in params) p[n] = params[n].call(this, d, i);
return _superformulaPath(p, segments.call(this, d, i), Math.sqrt(size.call(this, d, i)));
}
superformula.type = function(x) {
if (!arguments.length) return type;
type = d3.functor(x);
return superformula;
};
superformula.param = function(name, value) {
if (arguments.length < 2) return params[name];
params[name] = d3.functor(value);
return superformula;
};
// size of superformula in square pixels
superformula.size = function(x) {
if (!arguments.length) return size;
size = d3.functor(x);
return superformula;
};
// number of discrete line segments
superformula.segments = function(x) {
if (!arguments.length) return segments;
segments = d3.functor(x);
return superformula;
};
return superformula;
};
function _superformulaPath(params, n, diameter) {
var i = -1,
dt = 2 * Math.PI / n,
t,
r = 0,
x,
y,
points = [];
while (++i < n) {
t = params.m * (i * dt - Math.PI) / 4;
t = Math.pow(Math.abs(Math.pow(Math.abs(Math.cos(t) / params.a), params.n2)
+ Math.pow(Math.abs(Math.sin(t) / params.b), params.n3)), -1 / params.n1);
if (t > r) r = t;
points.push(t);
}
r = diameter * Math.SQRT1_2 / r;
i = -1; while (++i < n) {
x = (t = points[i] * r) * Math.cos(i * dt);
y = t * Math.sin(i * dt);
points[i] = [Math.abs(x) < 1e-6 ? 0 : x, Math.abs(y) < 1e-6 ? 0 : y];
}
return _line(points) + "Z";
}
var _superformulaTypes = {
asterisk: {m: 12, n1: .3, n2: 0, n3: 10, a: 1, b: 1},
bean: {m: 2, n1: 1, n2: 4, n3: 8, a: 1, b: 1},
butterfly: {m: 3, n1: 1, n2: 6, n3: 2, a: .6, b: 1},
circle: {m: 4, n1: 2, n2: 2, n3: 2, a: 1, b: 1},
clover: {m: 6, n1: .3, n2: 0, n3: 10, a: 1, b: 1},
cloverFour: {m: 8, n1: 10, n2: -1, n3: -8, a: 1, b: 1},
cross: {m: 8, n1: 1.3, n2: .01, n3: 8, a: 1, b: 1},
diamond: {m: 4, n1: 1, n2: 1, n3: 1, a: 1, b: 1},
drop: {m: 1, n1: .5, n2: .5, n3: .5, a: 1, b: 1},
ellipse: {m: 4, n1: 2, n2: 2, n3: 2, a: 9, b: 6},
gear: {m: 19, n1: 100, n2: 50, n3: 50, a: 1, b: 1},
heart: {m: 1, n1: .8, n2: 1, n3: -8, a: 1, b: .18},
heptagon: {m: 7, n1: 1000, n2: 400, n3: 400, a: 1, b: 1},
hexagon: {m: 6, n1: 1000, n2: 400, n3: 400, a: 1, b: 1},
malteseCross: {m: 8, n1: .9, n2: .1, n3: 100, a: 1, b: 1},
pentagon: {m: 5, n1: 1000, n2: 600, n3: 600, a: 1, b: 1},
rectangle: {m: 4, n1: 100, n2: 100, n3: 100, a: 2, b: 1},
roundedStar: {m: 5, n1: 2, n2: 7, n3: 7, a: 1, b: 1},
square: {m: 4, n1: 100, n2: 100, n3: 100, a: 1, b: 1},
star: {m: 5, n1: 30, n2: 100, n3: 100, a: 1, b: 1},
triangle: {m: 3, n1: 100, n2: 200, n3: 200, a: 1, b: 1}
};
d3.superformulaTypes = d3.keys(_superformulaTypes);
})();


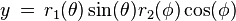




.jpg)
你在做一件神奇的事情 赞